2D Aristotelian diagrams

This page provides a number of 2D Aristotelian diagrams that can be constructed with bitstrings of length 4 (the bitstring representation format is introduced here; more details can be found in Paper P7 and Paper P10). Based on the types of bitstrings they contain, we distinguish various families of:

Aristotelian squares (or squares of oppositions),
Aristotelian hexagons (or hexagons of oppositions),
Aristotelian octagons (or octagons of oppositions).

For the visual representation of the Aristotelian relations we use the following two colour and line coding systems: $colour codes$

Aristotelian squares

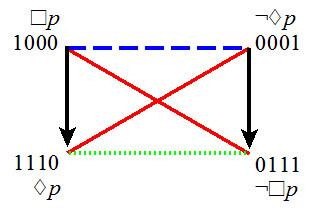
balanced classical square — **classical square**

2 bitstrings of level 1

2 bitstrings of level 3

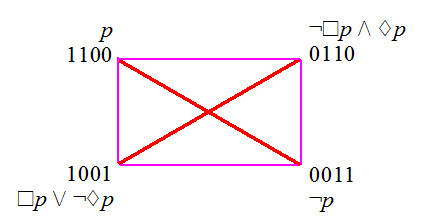
balanced degenerated square — **degenerated square**

4 bitstrings of level 2

Aristotelian hexagons

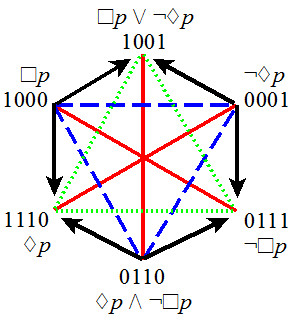
JSB strong hexagon — **Sacoby-Sesmat-Blanché hexagon (strong)**

2 bitstrings of level 1

2 bitstrings of level 2

2 bitstrings of level 3

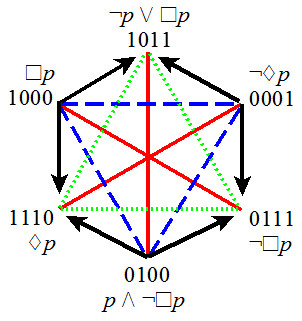
JSB weak hexagon — **Sacoby-Sesmat-Blanché hexagon (weak)**

3 bitstrings of level 1

3 bitstrings of level 3

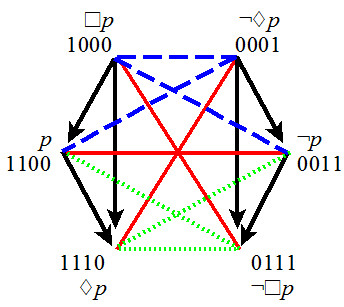
SC hexagon — **Sherwood-Czezowski hexagon**
(Moretti-Pellissier)

2 bitstrings of level 1

2 bitstrings of level 2

2 bitstrings of level 3

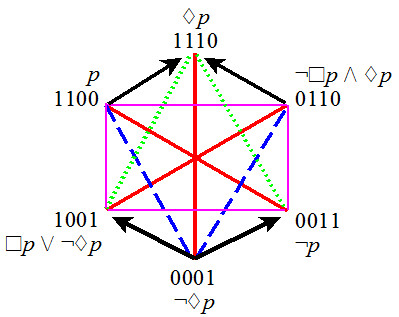
unconnected-4 hexagon — **Unconnected-4 hexagon**
(Smessaert-Demey)

1 bitstring of level 1

4 bitstrings of level 2

1 bitstring of level 3

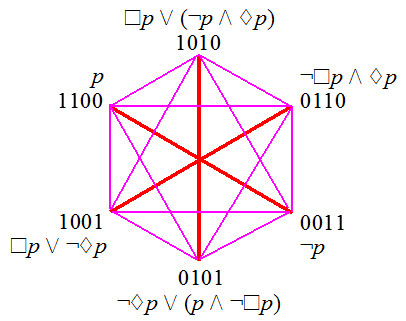
unconnected-12 hexagon — **Unconnected-12 hexagon**
(Smessaert-Demey)

6 bitstrings of level 2

Aristotelian octagons

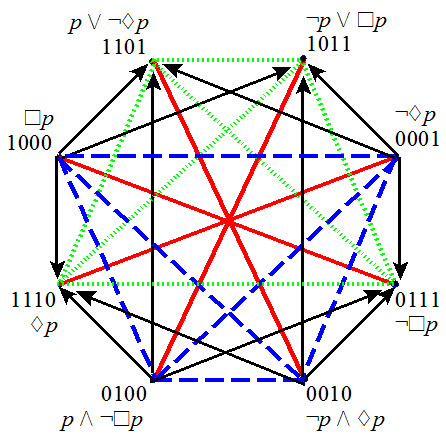
**Moretti-Pellissier octagon**

4 bitstrings of level 1

4 bitstrings of level 2

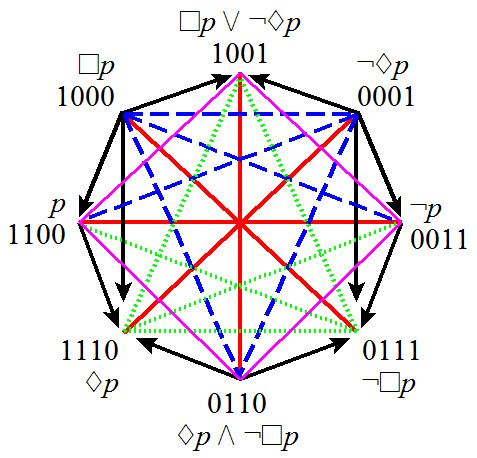
**Béziau octagon**

2 bitstrings of level 1

4 bitstrings of level 2

2 bitstrings of level 3

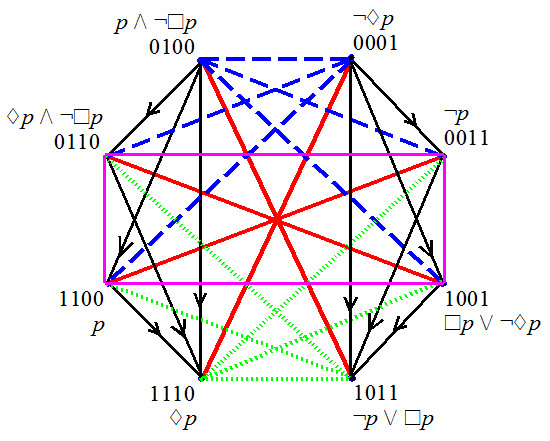
**Buridan octagon**

2 bitstrings of level 1

4 bitstrings of level 2

2 bitstrings of level 3